线性回归问题

线性回归问题即已知一系列样本的自变量和因变量的值，求解以下方程中的各θ_j：

$$h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2 + \cdots + θ_nx_n$$

设样本数量为m，评估拟合的直线与实际样本之间差异的代价函数（Cost Function）为：

$$J(θ_0,θ_1,\cdots,θ_n) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})^2$$

因此，寻找最佳拟合的线性回归模型则转化为求解该代价函数的最小值，常用方法为最小二乘法（Least Squares Method）和梯度下降法（Gradient Descent Method）。

这里以一元线性回归为例，分别使用最小二乘法和梯度下降法进行线性回归，使用的语言为Octave/MATLAB。首先准备样品的数据集：

X = [ones(100, 1), [1:100]']; % 构建一个100×2的因变量x的矩阵，第一列都为1（x_0=1）
randn("seed", 123); % 设定randn的seed为123，方便后面重现随机过程
% 按照方程y = 2x + 200（即θ_0=200, θ_1=2）生成因变量，并加上随机抖动：
y = ([1:100]'+10*(randn(100, 1)))*2+200;
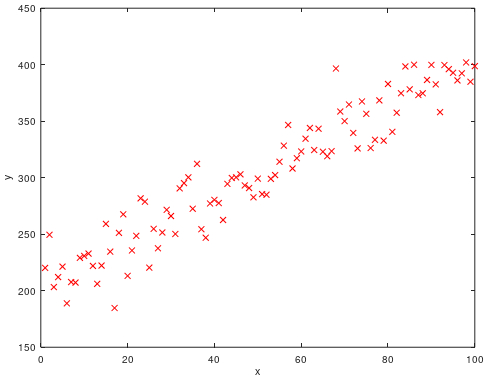
plot(X(:,2), y, 'rx'); % 绘制点图
xlabel('X');
ylabel('y');
hold on;

其中X为自变量组成的设计矩阵，行对应各样本，列对应各特征；y为因变量组成的矢量：

$$ X = \begin{bmatrix} {1}&{(x_{1}^{(1)})}&{\cdots}&{(x_{n}^{(1)})}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {1}&{(x_{1}^{(m)})}&{\cdots}&{(x_{n}^{(m)})}\\ \end{bmatrix} ;\ y = \begin{bmatrix} {y^{(1)}}\\ {\vdots}\\ {y^{(m)}}\\ \end{bmatrix} $$

得到点图如下所示：

使用最小二乘法求解线性回归问题

最小二乘法是将代价函数的每个θ的偏导数设为0（一元线性回归时即为全导数），通过得到的正规方程求解各θ的值：

$$set:\ \frac{∂}{∂θ_j}J(θ) = 0$$

可得到求解θ的正规方程组为：

$$θ = (X^TX)^{-1}X^Ty$$

因为是直接计算不需要迭代，因此代码很简单，一行就搞定：

theta = pinv(X'*X)*X'*y; % pinv函数为求解伪逆矩阵，在这个简单的例子里用inv也可以
plot(X(:,2), X*theta, 'g'); % 用绿色的直线绘制拟合的函数

可得到θ的计算结果为[203.6221; 1.9871]，即拟合的公式为y = 1.9871x + 203.6221，如下图：

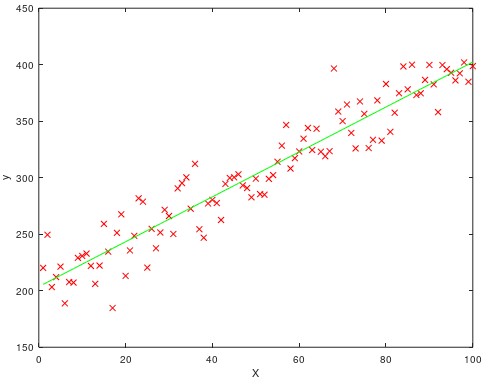
需要注意的是：

• X^TX通常情况下是可逆的。如果遇到不可逆的情况，检查是否有冗余的特征，或者特征数量太多。
• 因为公式中进行了3次X矩阵（或其转置、逆矩阵）相乘，因此最小二乘法的复杂度大体可表示为：O(n³)。虽然最小二乘法可以直接计算代价函数的最小值，但是当样本数n非常大时，速度就会变得很慢。这时候我们可以使用梯度下降法来解决线性回归的问题。

使用梯度下降法求解线性回归问题

梯度下降法将线性回归问题形象化为一个“下山问题”。从一组设定的θ开始，通过调整θ的值逐步减小代价函数的值，最终得到代价函数的局部最小解（即回归模型的局部最优解）。因为线性回归的代价函数总是凸函数，所以局部最优解即为全局最优解。调整θ的方法为每次迭代时每个特征所对应的θ同时减去学习率α乘以代价函数的偏导数：

$$ \begin{align} repeat &\{ \\ & θ_j := θ_j - α\frac{∂}{∂θ}J(θ) = θ_j - α\frac{1}{m}\sum_{i=1}^{m}(h_θ(x^{(i)}-y^{(i)}))x_j^{(i)} \\ & \} \ (同时更新：j = 0,\cdots,n)\\ \end{align} $$

代码实现如下：

% 定义函数gd，用于计算每轮迭代用于更新θ的矢量
function r = gd(m, X, y, alpha, theta)
  predictions = X * theta;
  r = alpha*(1/m)*(X'*(predictions-y));
endfunction

theta = [0; 0]; % 初始化theta，这里设定为[0; 0]
alpha = 0.0005; % 设定学习率为0.0005
m = size(X, 1); % m为训练样本数，在这里即100

% 进行100000次迭代
for n = 1:100000,
  r = gd(m, X, y, alpha, theta);
  theta = theta - r; % 更新θ
  disp(theta');
end;
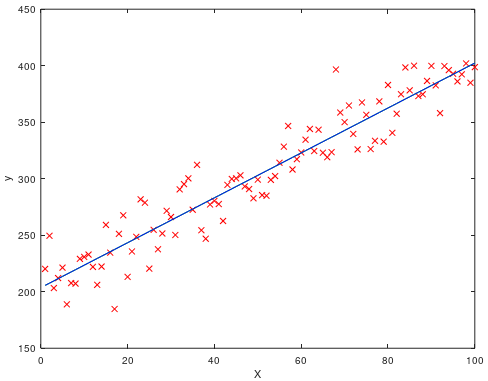
plot([1:100], [1:100]*theta(2)+theta(1), 'b'); % 用蓝色的直线绘制拟合的函数

经过100000轮迭代后最终得到θ的计算结果为[203.6212; 1.9871]，与上面最小二乘法计算出来的[203.6221; 1.9871]非常接近。从图中也可以看出，梯度下降法拟合的直线基本上遮住了最小二乘法求解的直线：

附录

代价函数的计算：

function J = calCostFunction(X, y, theta)
  predictions = X * theta;
  m = size(X, 1);
  J = 1/(2*m)*sum((predictions-y).^2);
endfunction

参考资料：

吴恩达机器学习课程：https://study.163.com/course/courseLearn.htm?courseId=1004570029